🪴 l4rk's Quartz

06数理统计的基本概念

12分钟阅读

样本的二重性
设 为从总体 中抽取的样本
样本具有{随机变量}的性质,{数}的性质

Q: 为从总体 中抽取的样本
为什么样本具有二重性 (随机变量与数的性质)?
A: 随机变量: 在未确定之前, 是一组随机变量
数: 在确定之后 为一组数, 自然有数的性质

简单随机样本的要求
为从总体 中抽取的样本
之间{相互独立}且{同分布}

统计量有{二重性}(与样本相同的性质)

统计量的本质是{函数 }
为{自变量}
观测值本质是{函数值 }
为{确定的值}

常见的统计量
样本均值 {}
样本方差 {} = {}

统计量之间的独立性
一般来说统计量之间{不是}相互独立

Q: 为什么样本方差
系数是 , 而不是 ?
A: 设真实的均值为
这里使用了 替代 , 而 是用 n 个样本算出来的. 这就导致了自由度的下降
例如如果有 3 个数据点, 我们知道了 和 , 那么 就必然等于
显然自由度为 2, 而不是 3
它天然地离样本数据点”更近”, 也就是说
, 如果 , 估计出来的方差会相较于实际情况偏小
需要修改参数, 放大结果, 更贴近实际, 这个系数恰好就是

统计量与数字特征的关系
{}
{}
{}

样本的 阶原点矩
样本的 阶中心矩

服从 的分布函数
{}
{}

分布形式自由度特性
{c1: } {c1: 平方个数} {c1: }
{c1: }
{c2: } {c2: 样本内平方级}分布函数对称
{c3: } {c3: 母中平方个数}
{c3: 子中平方个数}		 {c3: }

分布对于样本的要求

{相互独立}且均服从{标准正态分布 }

分布的定义
相互独立且均服从标准正态分布
{} 服从 , 自由度为{}

Q: 中的自由度 是什么?
A:
自由度 是独立变量的个数

Q: 什么时候使用卡方分布
A: 见到平方想卡方

三大分布, 概率密度函数的对称性
分布 {非对称}
分布 {对称}
分布 {非对称}

Q: 三大分布中,哪个分布的概率密度函数是对称的?
A: T分布

卡方分布的数字特征

{}
{}

卡方分布的可加性
且与相互独立, 则
{}

分布对于随机变量与样本的要求

随机变量 {} 样本 {}, 且 与 {相互独立}(独立性)

分布的定义

{} 服从 自由度为

分布与正态分布的关系
, 为 的概率密度
{} {}
{}

Q: 为什么 ?
A: 分布分子服从
分母
这里的 也服从
根据大数定律,当 时,一系列独立同分布随机变量的样本均值会收敛于其期望值.
当 时,样本均值 会(依概率)收敛于期望值

, 并且 .
因此 .

所以

分布与 分布的关系

{} {}

Q: 为什么
,
A:

分布对于样本的要求

{} {}, 且 与 {相互独立}(独立性)

分布的定义
, 且 与 相互独立
{}, 服从 , 第一自由度为 , 第二自由度为

分布的特性
{}

设 是来自正态总体 的一个简单随机样本
与 分别为样本均值和样本方差
{}
{} {}
{} {}

设 是来自正态总体 的一个简单随机样本
样本均值:
样本离差:
样本方差:
与 天然{相互独立}
与天然{相互独立}

设 是来自正态总体 的一个简单随机样本
样本离差:{}

设 是来自正态总体 的一个简单随机样本
与 分别为样本均值和样本方差
证明

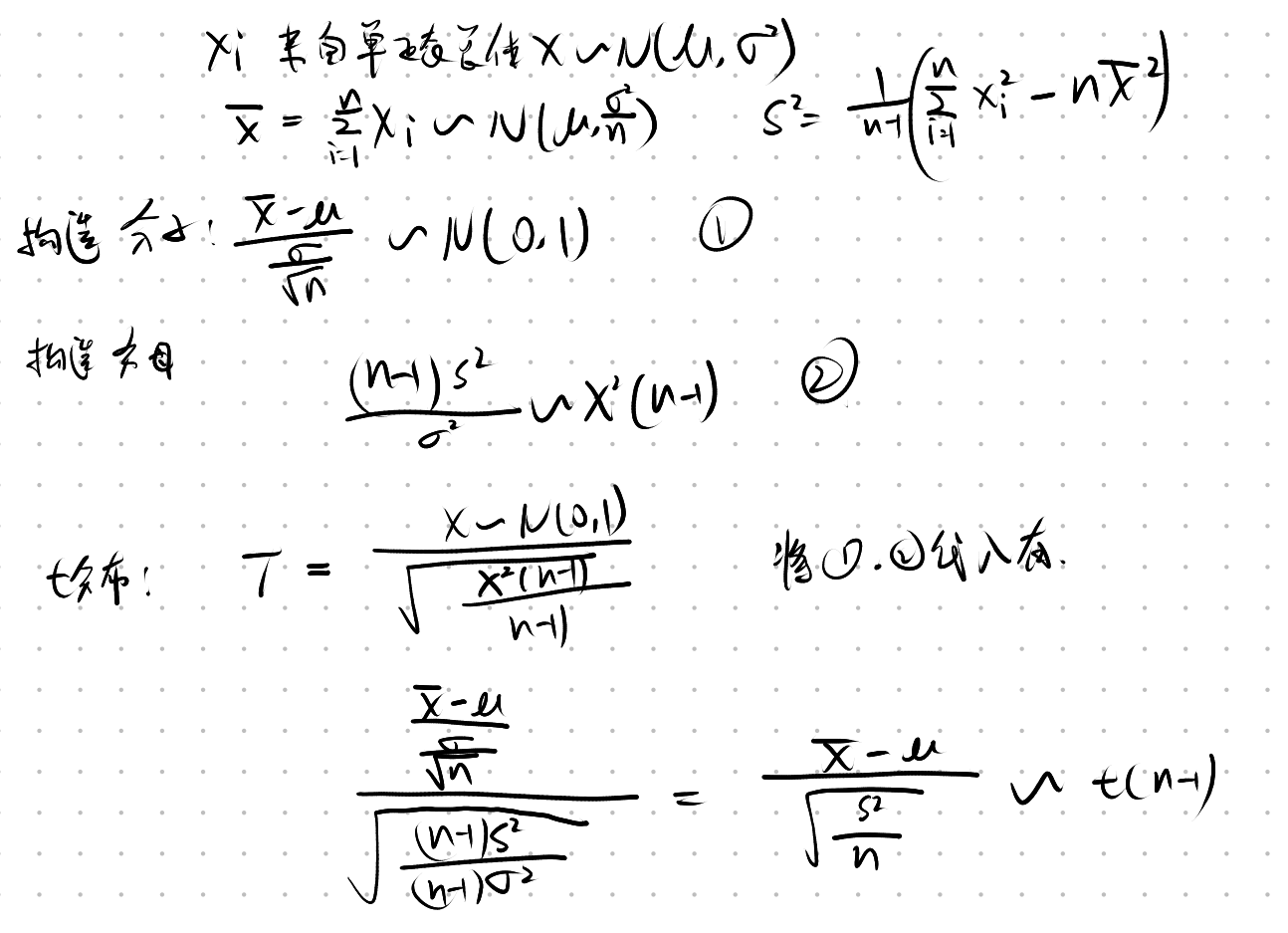
Q: 对于来自正态总体的样本, ,
其样本均值 与样本方差 是相互独立的吗?
A: 相互独立
证明比较复杂按下不表

Q: 在什么情况下
统计量样本均值 与样本方差 相互独立?
A: 仅在原始数据来自正态分布时

哪些可以得到卡方分布

,
,

样本方差 相关统计量的分布推导

  1. 构造卡方分布:
    我们知道 ,将其标准化得到 .
    根据卡方分布的定义,这 个独立标准正态变量的平方和服从自由度为 的卡方分布:
  2. 对平方和进行代数分解:
    这是最关键的一步,我们对求和项进行变换,引入样本均值 :

    展开这个平方项:



    我们来分析中间的交叉项:

    而 .
    所以,交叉项为 0.
    分解结果为:

  3. 两边同除以 :

    现在,我们用统计量的符号来重写这个等式:
  4. 分析等式中各项的分布:
    • 等式左边:我们已经知道,.
    • 等式右边第二项:我们刚在第一部分推导出 ,所以 .因此,它的平方 .
  5. 应用 Cochran 定理:
    我们有了一个形如 的结构,其中 ,.Cochran 定理告诉我们,等式右边的两项是相互独立的,并且自由度是可加的.
    因此,第一项 必须服从卡方分布,其自由度为 .
    即 .

T 统计量的分布推导

结论:

推导过程:
这个推导是 t 分布定义的一次完美应用.

  1. 回顾 t 分布的定义:
    ,其中 ,,且 独立.

  2. 寻找 Z 和 U:
    根据我们前面的推导:

    • 令 .我们知道 .
    • 令 .我们知道 .这里的自由度 .

  3. 检查独立性:
    根据关键的 Cochran 定理,样本均值 和样本方差 是相互独立的.因此,由它们构造出的 和 也是相互独立的.

  4. 代入 t 分布的定义公式:

  5. 化简表达式:
    我们来化简分母:
    (因为 S 和 都是标准差,为正数)

    现在,将化简后的分母代回原式:

  6. 得出结论:
    我们构造的表达式完全符合 t 分布的定义,并且化简后得到了我们想要的目标统计量.其自由度为 的自由度,即 .
    因此,.

这个结果的重大意义在于,构造出的统计量 中不含有未知的总体方差 ,只含有可以从样本中计算出的 ,这使得在 未知时对总体均值 进行区间估计和假设检验成为可能.

关系图谱