04随机变量的数字特征

数字特征的计算主要依靠
数字特征的性质进行化简计算
利用完备性计算 41.8

一维随机变量数学期望
离散型随机变量为
分布律为 ,

若无穷级数绝对收敛
{}

一维随机变量数学期望
连续型随机变量为
概率密度为

若反常积分绝对收敛
{}

二维随机变量数学期望
为二维离散型随机变量
分布律为

若无穷级数绝对收敛
{}

二维随机变量数学期望
为二维连续型随机变量
联合概率密度为
若反常积分绝对收敛
{}

数学期望的性质
为随机变量
为任意常数, 则

• {}
• {}
• {}
• 若 与 是相互独立, 则有 {}
• {} { 与 不相关}
• {}

Q: 若
的独立性与相关性如何?
A: 不一定独立
一定不相关

Q: 独立与相关的关系
A:

为随机变量
方差的定义 {}
方差的计算公式 {}
标准差 (均方差) {}

为常数

• {}
• {} , {}
• 对任意的常数 , 有 {}(大小关系)

随机变量
期望存在, 其方差{c1: 不一定}存在
方差存在, 则期望{c1: 必}定存在

={}(原始定义)
={}(cov 形式)
={}( 形式)

与 相互独立是 {充分不必要} 条件
与 不相关是 {充要}条件

若 与 是相互独立 (独立性) 的随机变量, 则
{}

的{充要}条件是 以概率 1 取得常数 {}

分布名称	符号	数学期望	方差	定义域
0-1 分布		{}	{}
二项分布		{}	{}
泊松分布		{}	{}
几何分布		{}	{}
超几何分布		{}	{}
均匀分布		{}	{}
指数分布		{}	{}
正态分布		{}	{}

Q: 哪个分布的期望与方差相同?
A: 泊松分布

{}

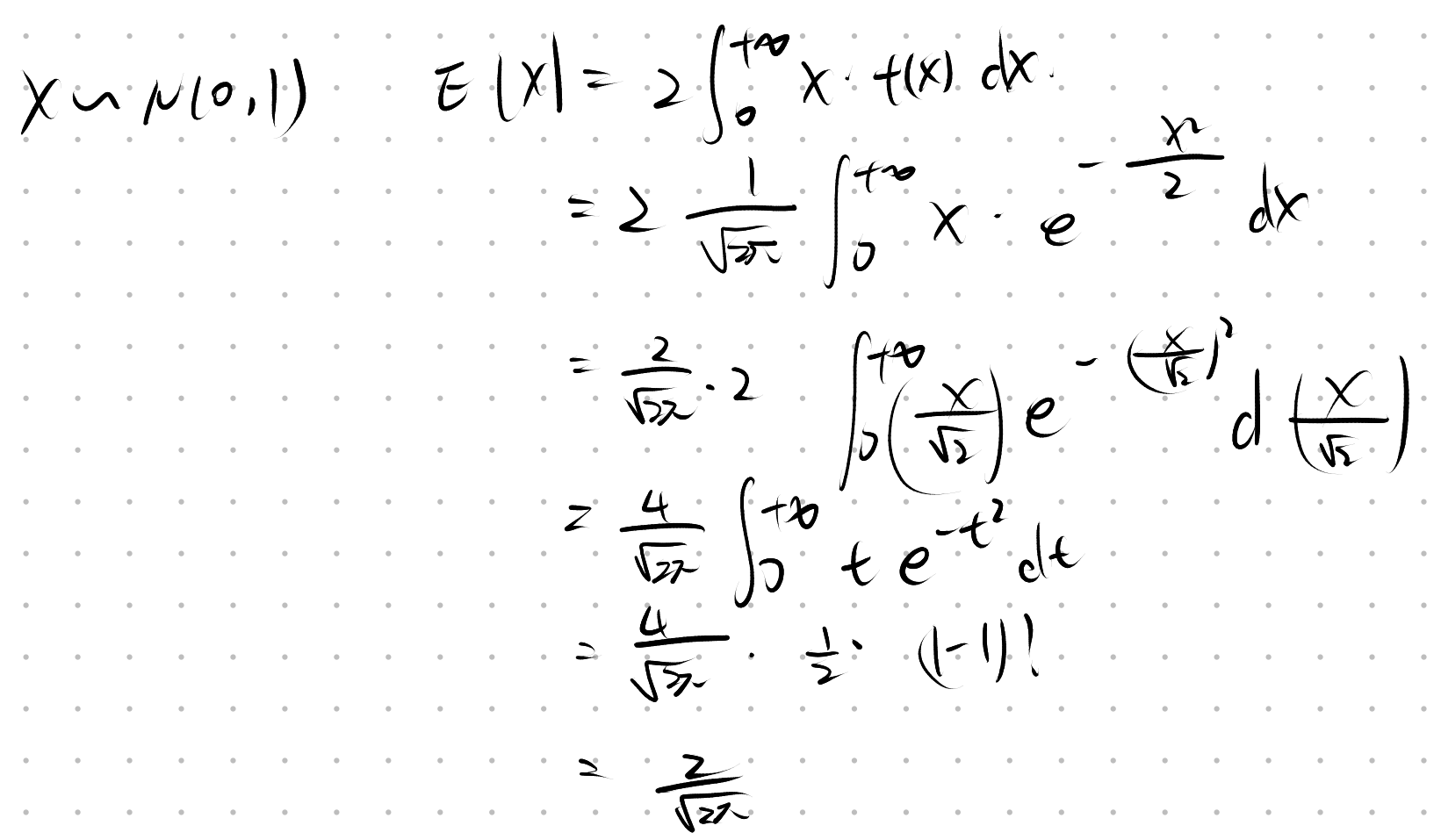
协方差的定义
{}

协方差的计算公式
定义推导:
{}
相关系数:
{}

{=}
{}
为任意常数 {}
是常数 {}
{}

协方差与独立
如果 与 独立, 则 {}

Q: 不相关与独立哪个条件更强?
A: 独立
不相关: 之间不存在直接的线性关系, 但可能存在非线性关系, 例如
独立: 之间不仅不存在直接的线性关系, 而且不存在非线性关系

随机变量 和 , 若
和 的相关系数 (使用 Cov 计算)
{}

相关系数的性质

的{充分必要}条件是: 存在常数 使
{}
当 (正相关) 时 { }
当 (负相关) 时 {}

随机变量 和 不相关, 即

{}
{}
{}

独立性与相关性的关系

• 一般情况下
  随机变量 和
  相互独立是不相关的{c1: 充分不必要}条件
• 特殊情况下
  随机变量 和 的联合分布是二维正态分布
  相互独立是不相关的{c1: 充要}条件

阶级原点矩与中心矩的定义
原点矩{}
中心矩{}

具有可加性的常见分布

• 只要相互独立就可以
  {c1: 正态分布}
  {c1: 泊松分布}
  {c1: 卡方分布}
• 既要相互独立也要同分布
  {c2: 二项分布}

Q: 对于独立同分布序列 , ,
什么是独立同分布的可加性?
A: 期望和方差具有可加性

混合期望计算公式
f(x) = p * f₁(x) + (1-p) * f₂(x)
E(X) = {p * E(X₁) + (1-p) * E(X₂)}

概率密度区间开闭性: {随意}
分布函数区间开闭性: {左开右闭}

Q: 为什么概率密度区间开闭性随意
A: 端点上是否有概率密度, 不会影响区间积分后, 分布函数的结果

Q: 为什么分布函数区间左开右闭
A: 分布函数的右连续性决定了区间左开右闭

随机变量 于区间上联合分布
相互独立的证明

• 不独立
  {举反例}
• 独立
  {}

大部分随机变量 都{没有}(有无) 独立性