随机试验
所有样本点
样本空间
事件的本质是{集合 (样本点
事件的运算规则和{集合}的运算规则相同
事件
在该次随机试验的结果样本点是否被事件
样本空间
空集
事件的运算
事件
互斥与相容
若事件
事件
事件的相互关系
事件
互逆事件是条件更加严格的{互斥 (不相容)}事件
Q: 对于事件 A, B, 互逆与不相容有什么区别?
A: 互逆: 要求
不相容: 仅要求
集合分配律
随机事件的运算规律就是集合的运算规律
要注意最重要的两个规律
吸收率和德摩根律
Q: 处理
A: 两 bar 变一 bar
一 bar 变零 bar
以
概率的公理化定义
- 非负性:{对于每一个事件 A, 有
} - 规范性:{对于必然事件
, 有 } - 可列可加性:{设
, 是两两互不相容的事件,即对于 , 有
, 则称 为事件 的概率}
条件概率定义为
乘法公式:
设
完备事件组的本质: 为样本空间
古典概型
几何概型
古典概型与几何概型的区别
- 古典概型
有{c1:有限}个样本点 (样本空间包含{c1:有限}个基本事件) - 几何概型
有{c2:无限}个样本点 (样本空间包含{c2:无限}个基本事件)
Q: 几何概型的计算方法, 映射法
A: 把
再把目标区间映射到相同坐标系上得测度为
概率为
设事件
有
则可以推出
设事件
则
翻译, 将文字语言转化为概率论语言
设事件
A, B 至少发生一个:{
A, B 同时发生:{
若 A 发生则 B 必发生:{
正向表达:
逆向表达:
概念公式:{
计算公式:{
概率不等式:
{
事件的独立性的定义
独立性不是语言中的”独立”
而是在描述一个相互关系
独立的传播性
对于事件
若两任意事件
若事件
Q: 如果两个随机变量
A: 相互独立
只要两个随机变量
任何只涉及
两两独立与相互独立的区别
对于事件
证明两独立只要证明
但是相互独立还要证明
Q: 证明
A: 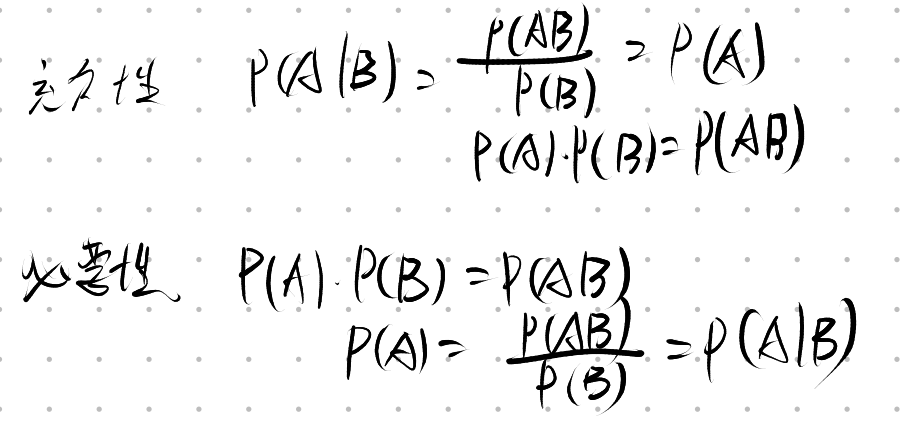
设事件
则
对于普通的随机事件
独立重复试验
一般地,在相同条件下重复做若干次的试验称为独立重复试验. 其中,各次试验的结果之间
{相互独立},且同一事件在各次试验中出现的概率相同
{伯努利试验}的定义
每次试验只有{对立}的两个结果
将每次试验只有对立的两个结果
设在
则在
条件概率的题目往往与{独立性}有关