常见的等价
{
Q: 如何将数据序列建成一个大根堆?
以序列 (6, 1, 5, 9, 8, 4, 7) 为例
A: “自底向上调整法”。
将原始序列看作一个完全二叉树。
从最后一个非叶子节点开始，向前逐个对每个节点进行“下沉（sift-down）”调整，使其满足大根堆的性质。
变化序列为
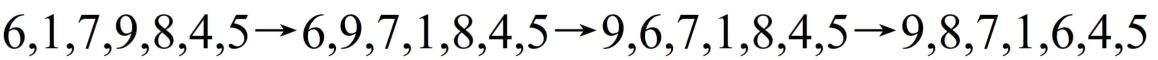
多叉树最优归并的虚段计算公式
Q: 叶节点权值分别为 2,3,4,5,6,7
进行三路归并
归并树为
A: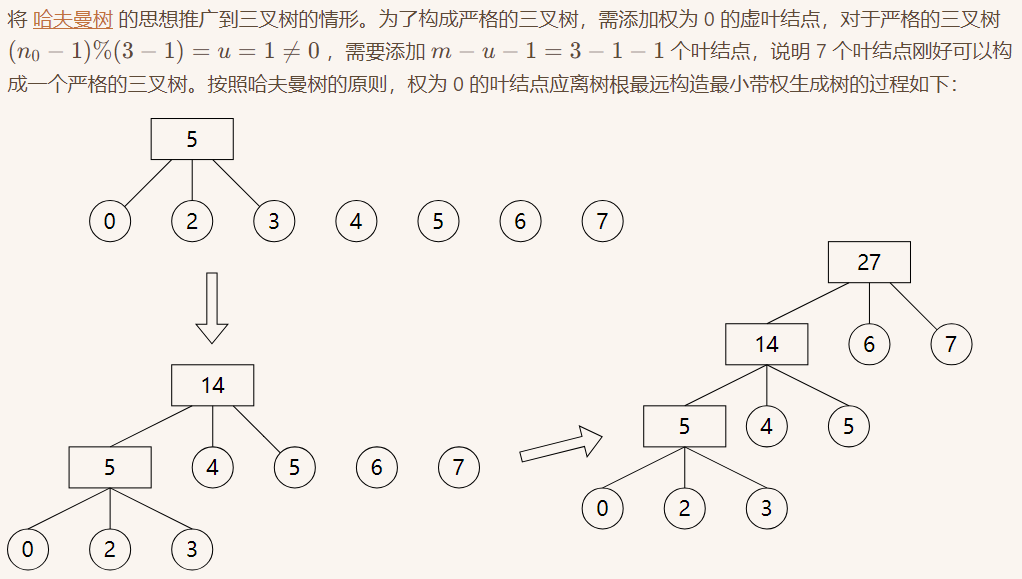 
Q: k 路归并, 叶节点数为 N, 如何判断是否需要添加虚段?
A: 计算
Q: k 路归并, 叶节点数为 N,需要添加的虚段的数量怎么算？
A:
Q: 为什么要用虚段？
A: 为了构建严格的k叉赫夫曼树
确保权值小的段处于树的最深层,从而使带权路径长度最小
Q: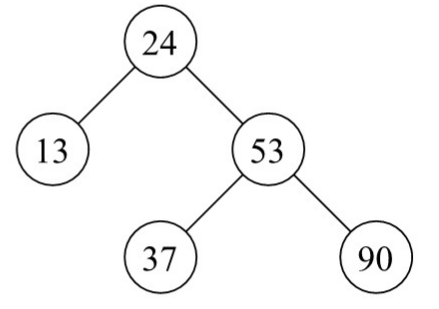 
在该平衡二叉树中插入关键字48后得到的新平衡二叉树为
A: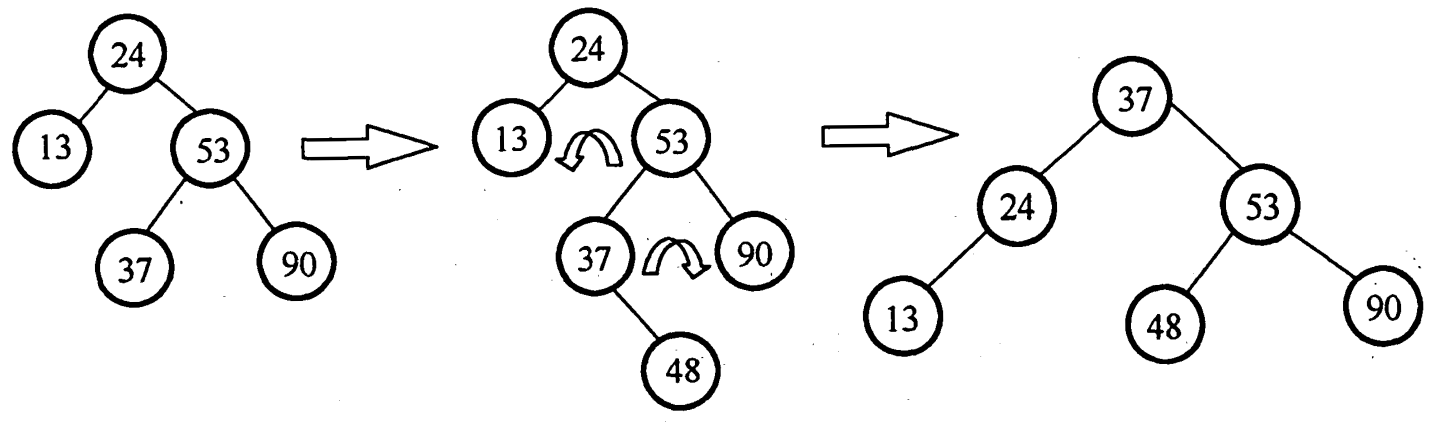 
Q: 画出该邻接多重表代表的无向图
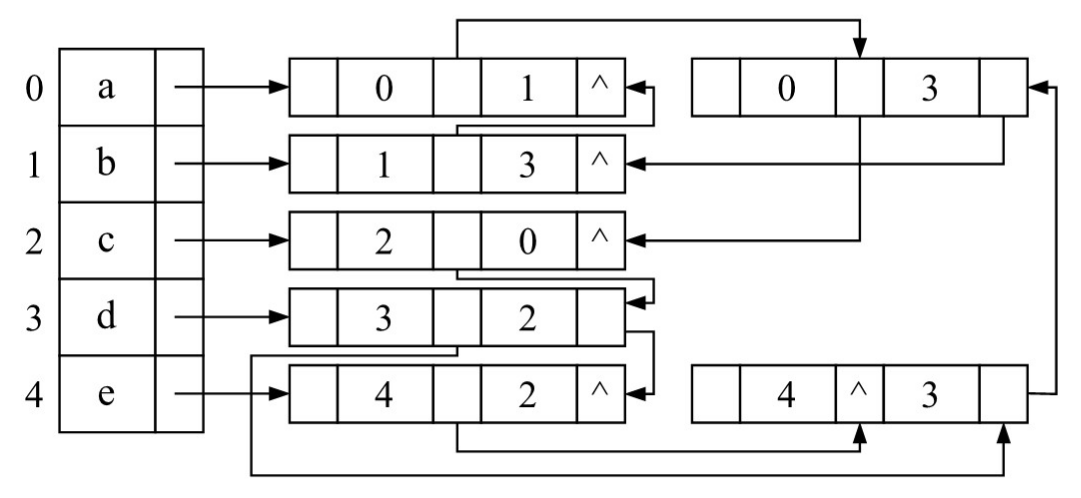
A: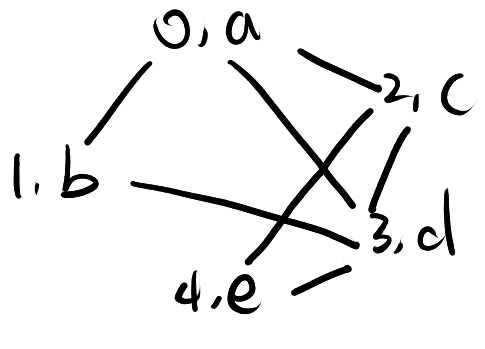 
Q: 依次将关键字 5, 6, 9, 13, 8, 2, 12, 15 插入初始为空的 4 阶 B 树
形成的B树为?
A: 