排序算法的平均最好时间复杂度为 {
是不是所有的排序都可以用顺序的存储方式?
排序的基本概念
Q: 排序算法的稳定性体现在哪里?
A: 具有相同关键字的两个元素
经过排序算法之后,
排序总结
稳定性:
总共五大类排序: 插入, 交换, 选择, 归并, 基数排序
不稳定: 希尔排序, 快速排序, 堆排序, 简单选择排序
稳定: 直接插入排序, 折半插入排序, 冒泡排序, 归并排序, 基数排序
冒泡排序、插入排序、希尔排序以及快速排序对数据的有序性比较敏感, 尤其是冒泡排序和插入排序;
选择排序不关心表的初始次序, 它的最坏情况的排序时间与其最佳情况没多少区别, 其比较次数为 n (n-1)/2, 但选择排序可以非常有效的移动元素. 因此对次序近乎正确的表, 选择排序可能比插入排序慢很多.
时间复杂度与初始序列关系:
无关: 简单选择排序, 堆排序, 归并排序, 基数排序
有关: 直接插入排序, 冒泡排序, 快速排序
特殊: 折半插入排序: 比较次数与初始序列无关, 元素移动次数与初始序列相关
希尔插入排序: 初始顺序确实有影响, 但间隔序列才是决定理论时间复杂度界限的最主要因素
快速排序: 标准快速排序的时间复杂度确实取决于初始序列的有序程度. 但现代健壮的实现方案会采用基准值选择策略 (如三数取中法或随机化) 来规避这种风险, 确保在几乎所有实际场景中都能保持良好性能.
简单选择排序: 比较次数与初始序列无关, 元素移动次数与初始序列相关
| 排序类别 | 具体算法 | 平均时间 | 空间 | 稳定性 | 与初始序列关系 | 移动次数 | 比较次数 |
|---|---|---|---|---|---|---|---|
| 插入排序 | 直接插入 | 稳定 | 有关 | 最少: 最多: | 最少: 最多: | ||
| 折半插入 | 稳定 | 移动次数无关, 比较次数有关 | 最少: 最多: | 恒为 (总是折半查找) | |||
| 希尔排序 | 不稳 | 有关 | 无法通过简单公式得出,依赖增量序列 | 无法通过简单公式得出 | |||
| 交换排序 | 冒泡排序 | 稳定 | 有关 | 最少: 最多: | 最少: 最多: | ||
| 快速排序 | 不稳 | 有关 | 随枢轴位置变化 | 随枢轴位置变化 最坏: | |||
| 选择排序 | 简单选择 | 不稳 | 比较次数无关, 移动次数有关 | 最少: 最多: | 恒为 (无论是否有序都要比完) | ||
| 堆排序 | 不稳 | 无关 | |||||
| 其他 | 归并排序 | 稳定 | 无关 | ||||
| 基数排序 | 稳定 | 无关 | 0 (无关键字比较) |
Q: 哪些排序的时间复杂度与初始序列有关?
A: 插入排序: 直接插入排序, 折半插入排序, 希尔排序
交换排序: 冒泡排序, 快速排序
Q: 哪些排序是稳定的?
A: 插泡归基
插入 (直接插入, 折半插入)
冒泡
归并
基数
时间复杂度
- 高手档 (
):
{“快归堆”:快速排序、归并排序、堆排序} - 平民档 (
):
{简单类算法:直接插入、折半插入、冒泡、简单选择} - 特殊档:
- 希尔排序:
(记住它是插入排序的改良,变快了) - 基数排序:
(线性时间,因为它不是基于比较的)
- 希尔排序:
空间复杂度
绝大多数排序都是原地工作 {
只需要记特殊的 3 个:{快速,归并,基数}
- 快速排序:{
.虽然是原地交换,但递归调用需要栈空间.} - 归并排序:{
.需要一个和原数组一样大的辅助数组来合并.} - 基数排序:{
.需要队列(桶)来暂存数据.}
- 完全无关(铁憨憨型):
- 简单选择排序:无论数据怎样,它都要走完双重循环去选最小值的下标.比较次数恒为
. - 归并排序:无论数据怎样,都要劈成两半再合并.
- 基数排序:只看位数,不看数值对比.
- 简单选择排序:无论数据怎样,它都要走完双重循环去选最小值的下标.比较次数恒为
- 比较次数无关,但移动次数有关:
- 折半插入:因为用二分查找确定位置,比较次数恒定为
,但插入时移动数据的次数取决于数据是否有序.
- 折半插入:因为用二分查找确定位置,比较次数恒定为
- 密切相关(会偷懒型):
- 直接插入、冒泡:如果本来就有序,它们只需要
的时间(最好的情况). - 快速排序:最怕有序(或逆序),会退化成
(最坏的情况).
- 直接插入、冒泡:如果本来就有序,它们只需要
5. 比较次数与移动次数的极端值(细节)
这部分需要理解逻辑:
- 基数排序:比较次数 = 0.它是唯一一个不需要比较关键字大小的算法(分配+收集).
- 简单选择排序:
- 移动次数最少:甚至可能为 0(已经有序).
- 比较次数最傻:恒为
.
- 冒泡排序:
- 移动次数最多:最坏情况下(逆序),每次比较都要交换.一次交换通常需要 3 次移动(temp = a; a = b; b = temp;),所以系数是 3.
插入排序
直接插入排序
Q: 描述一下直接插入排序的核心操作.
A: 从未排序区取出一个元素, 与已排序区的元素从后向前逐一比较. 如果已排序区元素更大, 就将其向后移动, 直到遇到比该元素小的元素
直接插入排序的性能分析
空间复杂度:
时间复杂度 (最好, 最坏, 平均):
- 最好:
(数组已基本有序) - 最坏:
(数组逆序) - 平均:
稳定性: 稳定
适用性: 顺序存储和链式存储的线性表, 采用链式存储时无须移动元素.
折半插入排序
Q: 描述一下折半插入排序的核心操作
A: 从未排序区取出一个元素, 与已排序区的元素根据折半查找的顺序比较. 直到找到合适的位置, 将该位置之后的元素向后移动, 再插入
Q: 直接插入排序和折半插入排序在元素移动次数和元素比较次数上有什么区别
A: 元素移动次数: 两者相等
元素比较次数: 直接插入排序与序列初始状态有关, 时间复杂度为
相较于直接插入排序边查找边移动, 折半插入排序 {c1: 比较}操作和{c1: 移动}操作分离..
折半插入排序的性能分析
时间复杂度 (最好, 最坏, 平均): 一般
空间复杂度:
稳定性: 稳定
适用性: 顺序存储的线性表
希尔排序
因为直接插入排序仅适合在基本有序的排序表, 所以提出希尔排序
Q: 描述一下希尔排序的核心操作
A: 先将待排序表分割成若干形如
希尔排序的性能分析
空间复杂度:
时间复杂度 (最坏, 序列长度在一定范围内):
- 最坏:
- 序列长度在一定范围内:
稳定性: 不稳定
适用性: 顺序存储的线性表
交换排序
冒泡排序
Q: 描述一下冒泡排序的核心操作
A: 从后往前 (或从前往后) 两两比较相邻元素的值, 若为逆序 (即
冒泡排序的性能分析
空间复杂度:
时间复杂度 (最好, 最坏, 平均):
- 最好:
(序列基本有序) - 最坏:
(序列逆序) - 平均:
稳定性: 稳定
适用性: 顺序存储和链式存储的线性表.
快速排序
Q: 描述一下快速排序的核心操作
A: 分治法
在待排序表
然后分别递归地对两个子表重复上述过程, 直至每部分内只有一个元素或为空为止, 即所有元素放在了其最终位置上.
快速排序的性能分析
空间复杂度 (递归栈的深度) (最好, 最坏, 平均):
- 最好:
- 最坏:
- 平均:
时间复杂度 (最好, 最坏, 平均): - 最好:
(每次都是平衡划分) - 最坏:
(序列基本有序或者基本逆序) - 平均:
稳定性: 如果右端存在两个小于基准的相等关键字, 不稳定
适用性: 仅适用于顺序存储的线性表
Q: 哪个算法是内部排序算法中平均性能最优算法?
A: 快速排序
Q: 为什么快速排序是内部排序算法中平均性能最优算法?
A: 虽然快速排序算法的最好情况时间复杂度不是最小的, 但是平均时间复杂度与其最好时间复杂度很接近, 而不是接近其最坏情况下的运行时间
有多种方式可以保证快速排序中的最坏情况基本不会发生
例如:
- 从序列的头尾及中间选取三个元素, 再取这三个元素的中间值作为最终的枢轴元素
- 随机地从当前表中选取枢轴元素
Q: 若有 16 个不同的元素, 进行递归排序, 最好的递归次数与最差的递归次数, 分别为
A:
选择排序
简单选择排序
Q: 描述一下简单选择排序的核心操作
A: 假设排序表为
简单选择排序的性能分析
空间复杂度:
时间复杂度:
稳定性: 不稳定
适用性: 顺序存储和链式存储的线性表, 以及关键字较少的情况
元素间比较的次数与序列的初始状态无关
堆排序
小根堆的定义:
为一棵{c1: 二叉}树
并且对于序列中的元素
Q: 描述一下堆排序的核心操作
A: 首先将存放在
堆排序的性能分析
空间复杂度:
时间复杂度 (平均, 最坏, 最好): 三种情况下, 均为
稳定性: 不稳定
适用性: 序存储的线性表. 关键字较多的情况
Q: 每一次堆排序都能确定一个元素的位置吗?
A: 每次排序都将根节点与表尾结点交换, 确定其最终位置
归并排序, 基数排序和计数排序
归并排序
Q: 描述一下归并排序的核心操作
A: 归并的含义是将两个或两个以上的有序表合并成一个新的有序表. 假定待排序表含有
归并排序的性能分析
空间复杂度:
时间复杂度 (平均, 最坏, 最好):
稳定性: 稳定
适用性: 序存储和链式存储的线性表.
基数排序
Q: 描述一下基数排序的核心操作
A: 先排低位再排高位
每次收集之后再排序
Q: 对 110,119,007,911,114,120,122 进行基数排序
A: 
冒泡排序的性能分析
空间复杂度:
时间复杂度 (平均, 最坏, 最好):
稳定性: 稳定
适用性: 序存储和链式存储的线性表.
计数排序
Q: 描述一下计数排序的核心操作
A:
各种内部排序算法的比较
外部排序
Q: 对这五个段进行归并排序
生成第一次归并时的败者树
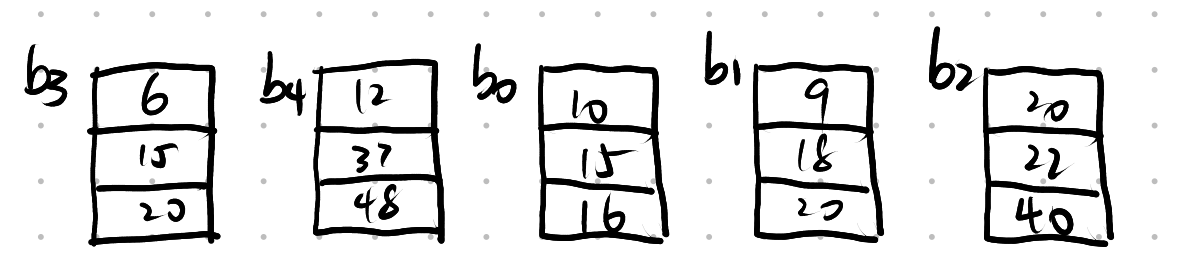
A: 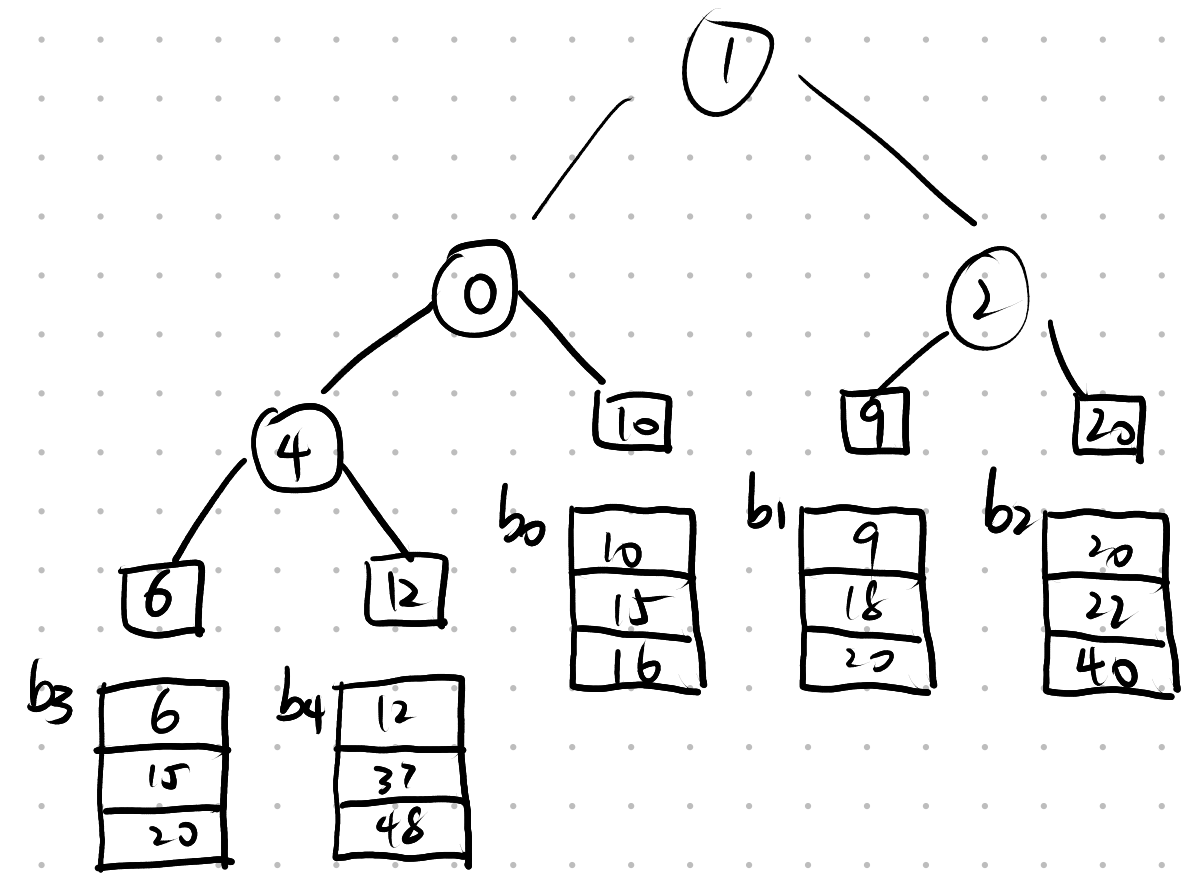
Q: 败者树
第一次归并的结果为

则第二次归并结果为
A: 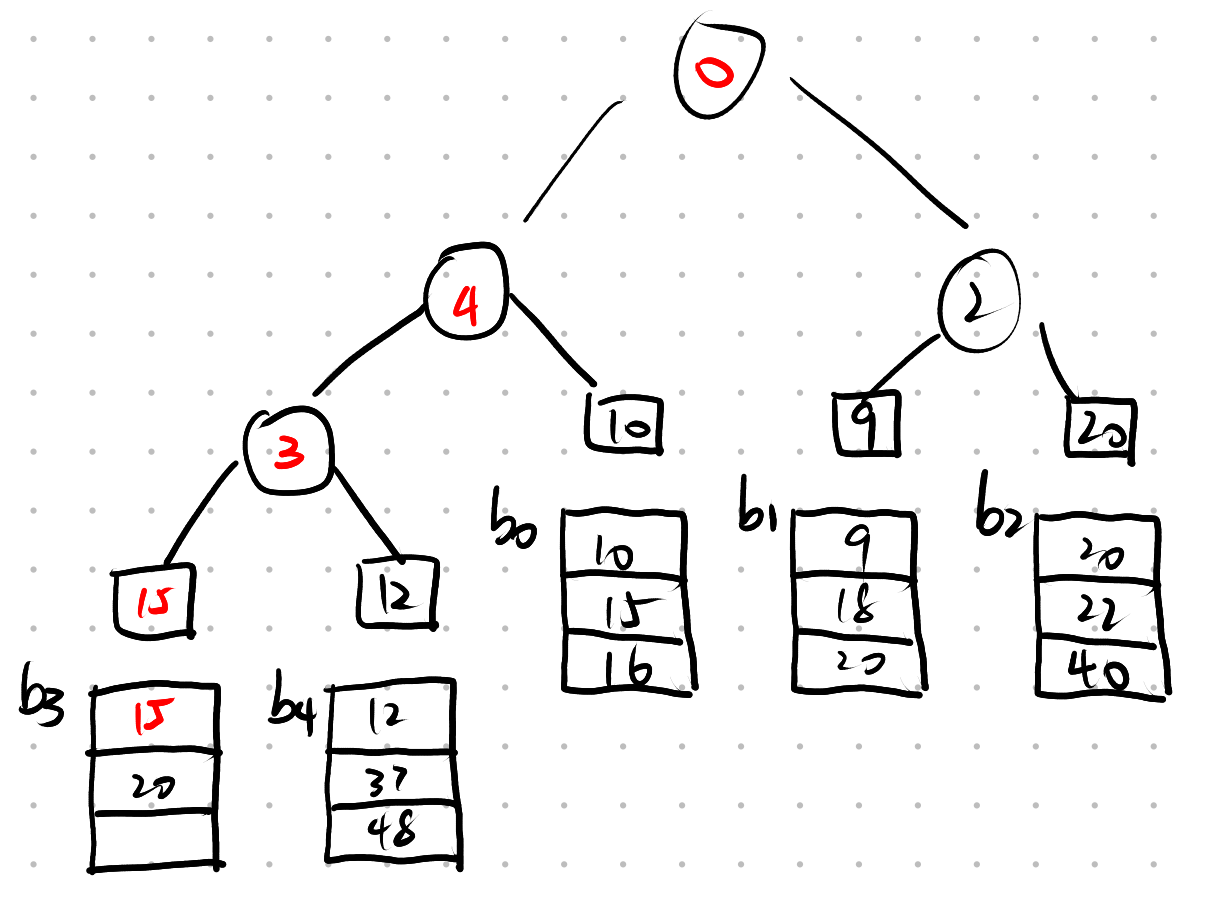
败者树分支结点中存储的是{较大}元素的{归并段段}号
冠军结点保存的是{胜者(最小关键字)}的{归并段段}号
Q: 一句话概括败者树的机制
A: 胜者(较小)者继续比较,败者(较大者)留下(段号)