03二维随机变量及其分布

设 为二维随机变量, 对任何实数 , 称二元函数
{}(P 形式),
为 的{联合分布函数}, 简称 的分布函数

二维随机变量联合分布函数的性质:

1. {}, {}
2. 二维随机变量 () 落在矩形区域 上的概率为
   {}
3. 与一维分布函数相同的单调不减,有界

二维边缘分布函数与联合分布函数间的关系 没有积分吗?
这我写的是啥啊?

二维离散型随机变量
条件分布律与联合分布律, 边缘分布律的关系
{}

设 () 为二维连续型随机变量
其概率密度为 , 边缘密度函数分别为 和
若 , 则
{}

二维连续型随机变量 ()
分布函数是 , 联合概率密度
{}

从联合概率密度 ,求分布函数 ,如何划分区域

1. 画出f(x,y)图像
2. 图像端点向右向上
   

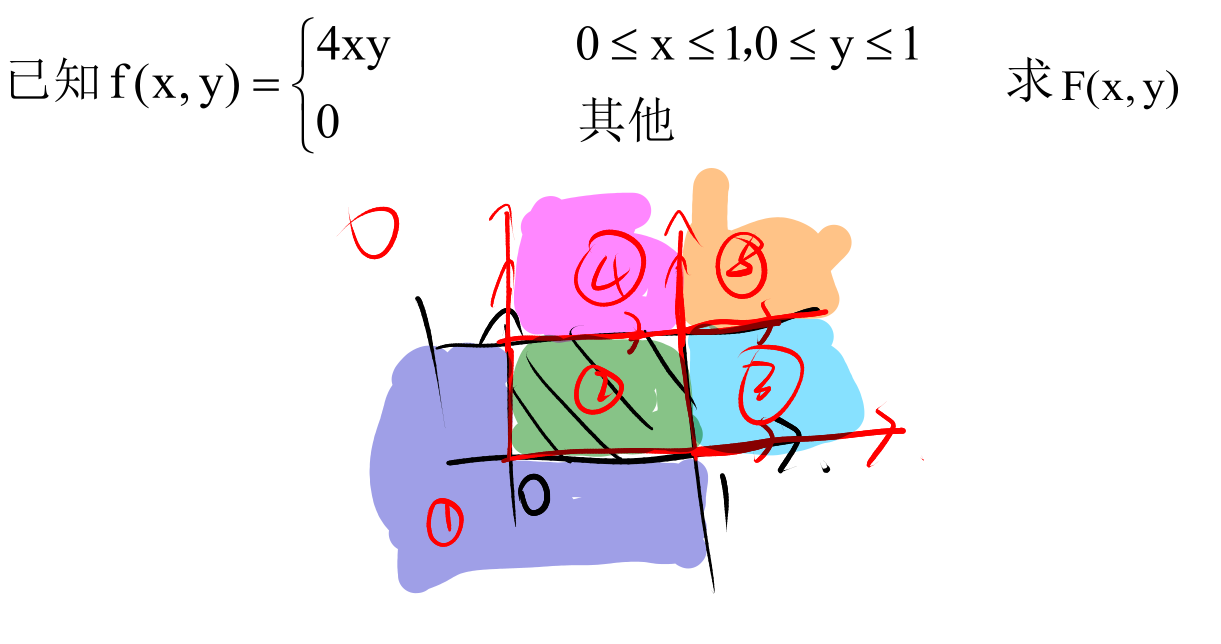
二维连续型随机变量 ()
分布函数是 , 联合概率密度
() 落在平面区域 内的概率为
{}

二维连续型随机变量 ()
分布函数是 , 联合概率密度
分布函数与联合概率密度的关系
在 处{连续}, 有
{}

设连续随机变量 ( 的概率密度为
边缘分布函数与联合分布函数的关系
{}{}
{}{}

设连续随机变量 ( 的概率密度为
边缘概率密度与联合概率密度的关系
{c1: }
{c1: }

二维连续型随机变量的条件概率分布函数计算公式
{}

二维随机变量独立性与分布函数
与 是相互独立, 则有
{}

是二维随机变量独立性的{充分必要}条件

独立的充要条件

• 二维离散型随机变量
  {}

独立的充要条件

• 二维连续型随机变量
  1. {c1: }
  2. 在点 处{c1: 连续}

对于二维离散型随机变量 , 若 与 相互独立, 则
{}
{}

对于二维连续型随机变量 (, 若 与 相互独立, 则
{}
{}

二维连续型随机变量 ( 服从区域 上的均匀分布
是平面上有界区域, 其面积为
则概率密度
{}

二维随机变量 联合分布于区域 均匀分布
区域 的形状为矩形, 三角形, 圆形
条件分布:{c1: 都是}(哪些是) 均匀分布
边缘分布:{关于坐标轴对称的矩形}(哪些是) 均匀分布

二维均匀分布的随机变量 的独立性与分布区间形状的关系
若 在 矩形区域 均匀分布, 则
与 {可能相互独立, 还需要看矩形是否与坐标轴对称}
若 在 圆形区域 均匀分布, 则
与 {不独立}

二维正态

Q: 设X,Y均服从正态分布,什么条件下
A: X,Y相互独立

两个边缘分布为{正态}分布，即

Q:
两个边缘分布为正态分布, 需要 为 吗?
A: 不需要
不论相关系数取到多少,边缘分布始终都是正态分布

与 {相互独立/不相关}的充分必要条件是 {}

独立与相关的本质
独立:
两个变量独立,意思是它们之间没有{任何}关系
不相关:
两个变量不相关,意思是它们之间没有{线性}关系

Q:
在什么情况下, 与 的非零线性组合 仍然服从二维正态分布
A:

,不全为0
{⇐>}

与 的线性组合 {服从}一维正态分布
{ }

当 与 {相互独立}时，有
{}

则 {} 是 相互独立的{充要}条件

高维包含了低维的信息, 能够轻松展开到低维
但是低维收缩到高维的时候, 经常会信息不足, 不能够全面描述高维的情况

二维离散型随机变量函数
设 , 则 的分布律为
{}

Q: 对于离散与连续组合的分布函数
设 的分布律为 为连续型随机变量
, 则 的分布函数
A: 定义, 拆离散, 找关键

二维随机变量函数的概率密度之卷积公式
若 的形式比较简单
将 改为
{}

二维连续型随机变量函数
设 的概率密度为 , 则 的分布函数为
{}
若 仍为{连续型随机变量}，则 的概率密度 {}

二维随机变量函数概率密度的方法
直接 {卷积公式}
间接 {二重积分求分布函数再对分布函数求导}