串的定义和实现
Q: 采用顺序存储的串 (如定长数组) 有什么主要弊端?
A: 会发生截断.
即当串的长度超过预定义的最大长度 (MAXLEN) 时, 超出的部分会被舍弃, 导致信息丢失.
串的模式匹配
Q: 对于主串长度为 n, 模式串长度为 m 的简单匹配(暴力匹配) 算法, 其最坏情况下的时间复杂度是多少?
A: O (nm)
Q: 对于主串长度为 n, 模式串长度为 m 的简单匹配 (暴力匹配) 算法, 其平均情况下的时间复杂度是多少?
A: O (n+m)
Q: 为什么 KMP 算法可以在
A: 整个匹配过程中, 主串始终没有回溯
Q: KMP 算法, 主串位置为 [i], 匹配串位置为 [j], 如果发生匹配失败, 主串位置与匹配串位置会发生怎样的变化?
A: 主串位置: [i] 不变, KMP 算法, 主串不会回溯
匹配串位置: j=next[j], 根据 next 数组的值, 修改匹配串位置
Q: KMP 算法中 next 数组的核心计算思想是什么?
A: 核心思想是计算模式串中每个子串的最长相等前后缀.
(具体计算方法较为复杂, 可参考相关视频或文章, 如: 前缀后缀比较)
Q: 计算字符串 abaabc 的 next 数组
A: 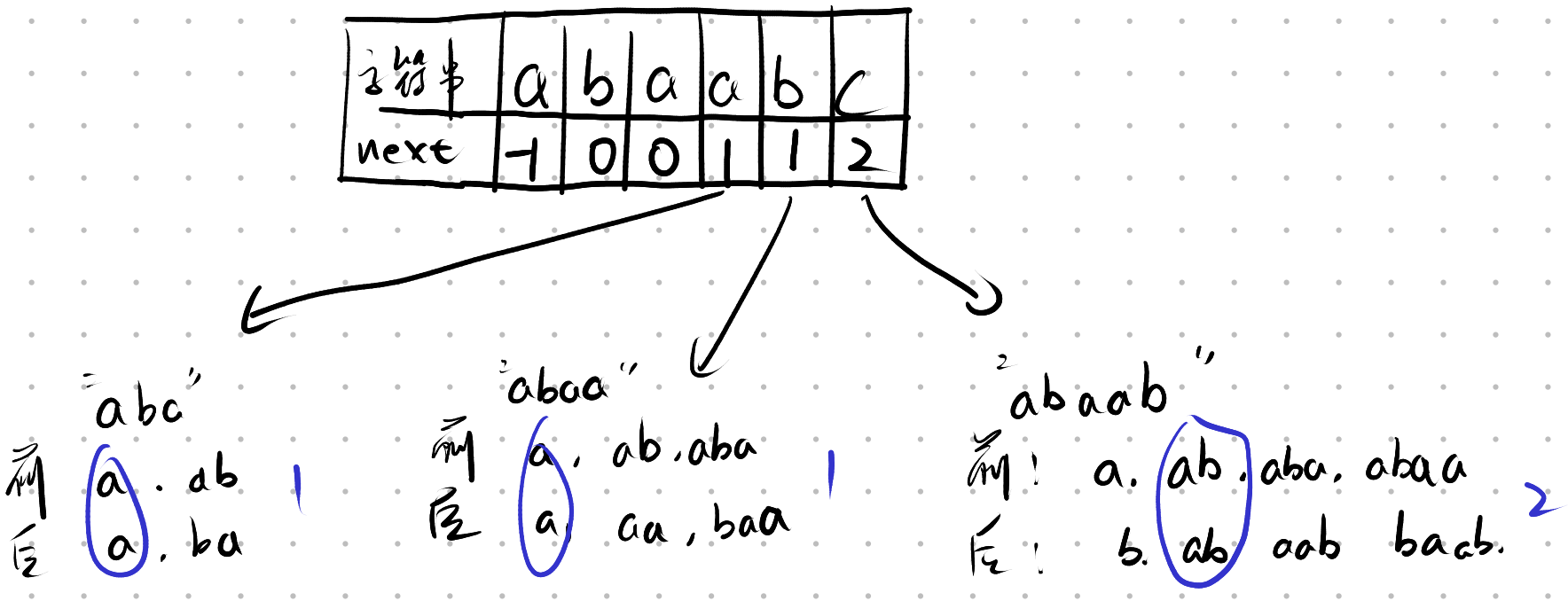
Q: KMP 算法的 next 数组优化为 nextval 数组, 目的是什么?
A: 避免在失配后, 跳转到的新位置的字符 p[next[j]] 仍然与当前失配字符 p[j] 相同, 从而导致不必要的重复比较.
Q: KMP 算法进一步优化
用 nextVal[n] 取代 next[n]
A: 用了递归判断, 第 i 个字符不匹配
比较第 next[i] 个字符与第 i 个字符是否相同
- 相同
next[i]=next[next[i]]
再次比较第next[i]个字符与第 i 个字符是否相同
进入递归直到第next[i]个字符与第 i 个字符不相同 - 不相同
next[i]不变